Contents
Tích phân là gì?
Khái niệm tích phân được sử dụng rất phổ biến trong toán học, nghịch đảo của vi phân chính là tích phân. Đây là 2 phép tính nền tảng rất quan trọng trong toán giải tích.
Khái niệm tích phân là gì được tách nghĩa theo tiếng Hán như sau:
- Tích – trong “tích cóp”
- Phân – chia từng phần nhỏ
Qua cách tách nghĩa như trên, ta có thể hiểu sơ qua “tích phân” là tổng của nhiều phần nhỏ.
Còn trong toán học, tích phân là gì?
– Cho hàm số f(x) liên tục trên một khoảng xác định (kí hiệu K), với hai số thực a và b bất kỳ nằm trong khoảng K này. Nếu F(x) là một nguyên hàm của f(x) thì F(b) – F(a) lúc này sẽ được gọi là tích phân của f(x) trong khoảng từ a đến b. Ký hiệu như sau:

Trong đó:
- ∫: là tích phân
- f(x)dx: là biểu thức nằm trong dấu tích phân
- dx: biến của tích phân
- Tính chất cơ bản của tích phân là gì?
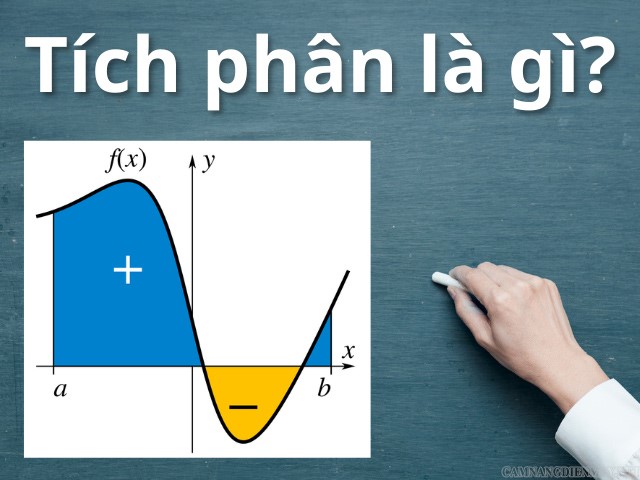
Người ta có thể thay đổi biểu thức f(x)dx bằng biểu thức như f(t)dt, f(y)dy, f(u)du… Ký hiệu này dùng để biểu thị ý nghĩa diện tích của một vùng năm trong không gian mặt phẳng xy, được bao quanh đồ thị của hàm f, trục hoành và các đường thẳng lần lượt là x = a; x = b sao cho các vùng nằm trên trục hoành được tính vào tổng diện tích còn phần dưới trục hoành sẽ được trừ vào tổng diện tích.
Xét F(x) là nguyên hàm của f(x) trong a và b. Khi đó tích phân bất định sẽ được biểu diễn như sau:
f(x)dx = F(x) + C
Khi ta gọi a là cận dưới của tích phân thì b sẽ là cận trên của tích phân đó.
=> Tổng quát khái niệm tích phân là gì: Cho một hàm số y = f(x) xác định và liên tục trên một đoạn [a;b], với F(x) là một nguyên hàm nào đó của hàm số y = f(x) trên [a;b]. Khi đó ta có:
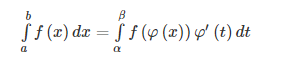
Tính chất của tích phân

Gọi f(x), g(x) lần lượt là các hàm số liên tục trên K. Cho a, b, c là những số nằm trong khoảng K. Khi đó, ta có các tính chất và của tích phân được biểu diễn như sau:
Các phương pháp tính tích phân
Bên cạnh khái niệm, tính chất tích phân là gì, ta cần nắm được các phương pháp xác định tích phân cụ thể để giải các bài toán liên quan. Sau đây là tổng hợp 3 phương pháp tính tích phân mà người học cần nắm rõ:
Phương pháp đổi biến số
– Cho hàm số f(x) liên tục trên đoạn [a;b], giả sử hàm số x = (t) có đạo hàm liên tục trên đoạn [α;β] [α;β] sao cho φ(α)=a, φ(β)=b φ(α)=a, φ(β)=b và a ≤ φ(t) ≤ b, a ≤ φ(t) ≤ b với mọi t ∈ [α;β].
Khi đó ta có:
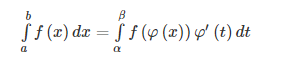
– Phương pháp đổi biến số loại 1: t = t (x)
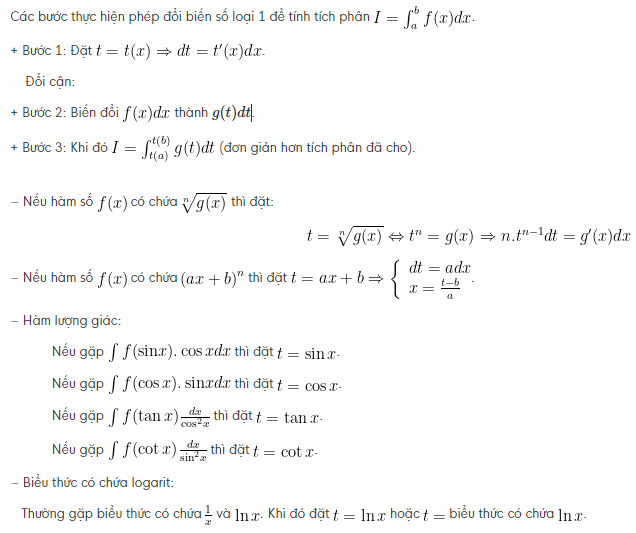
Phương pháp tính tích phân bằng các đổi biến số (loại 1)
Ví dụ:
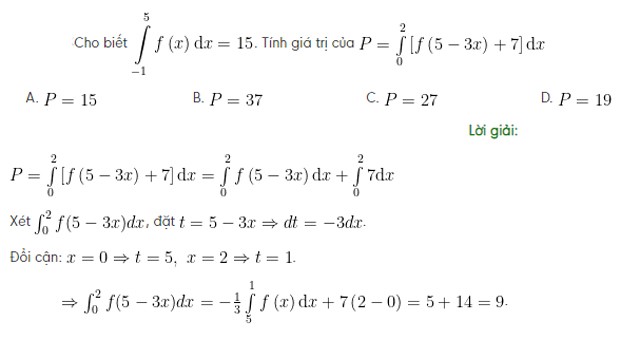
– Phương pháp đổi biến số loại 2: x = x(t)
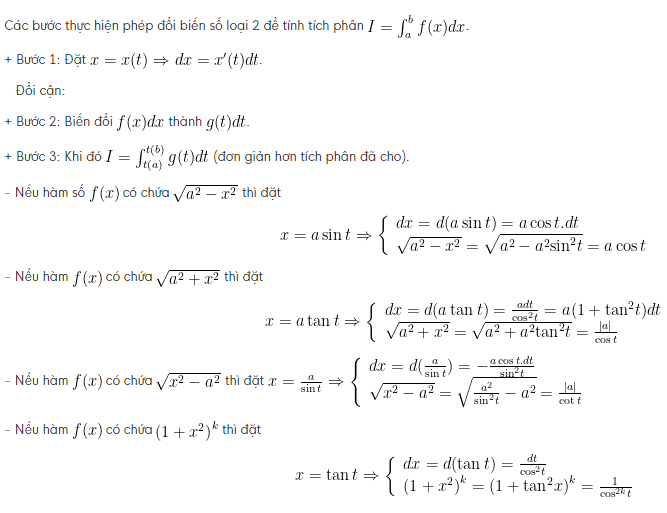
Phương pháp tính tích phân bằng cách đổi biển số (loại 2)
Ví dụ:

Phương pháp phân tích
Phương pháp phân tích là cách sử dụng đồng nhất các công thức để biến đổi biểu thức dưới dấu tích phân thành tổng của các hạng tử. Ví dụ:
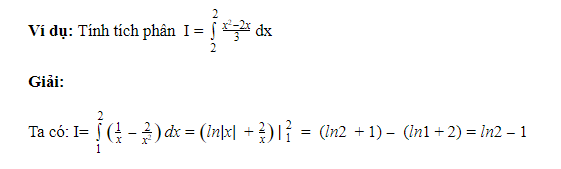
Phương pháp vi phân
Xét hàm số y = f (x) xác định trên tập D, vi phân của hàm số y sẽ được ký hiệu như sau:
dy = f’(x)dx hay d(f(x)) = f’(x)dx
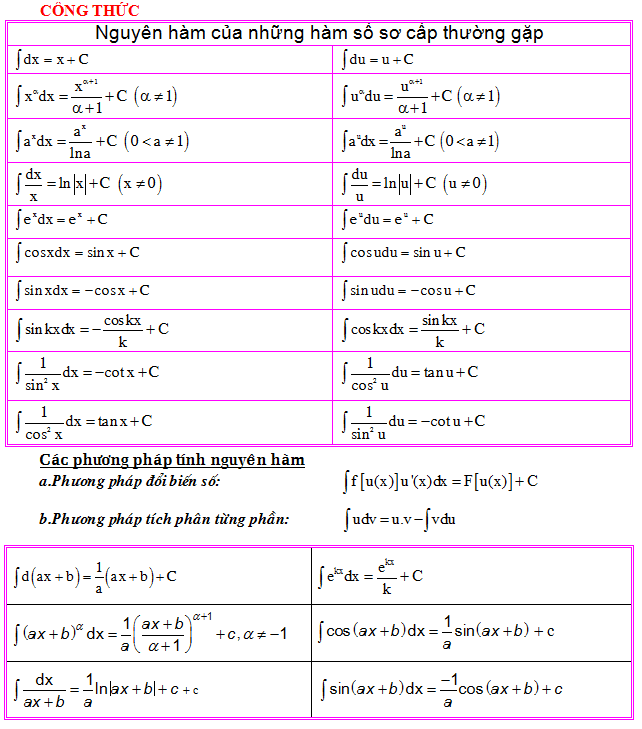
Để tính nhanh một tích phân bằng phương pháp vi phân, bạn cần ghi nhớ các công thức sau đây:
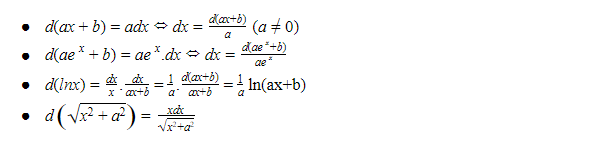
Tích phân từng phần
– Các bài tập về tích phân cần sử dụng tích phân từng phần khi hàm số dưới dấu tích phân là một trong các dạng sau đây:
- Là đa thức lượng giác
- Là đa thức mũ
- Là logarit đa thức
- Là đa thức có mũ – lượng giác
Lúc này, tích phân không sử dụng được hoặc rất khó sử dụng phương pháp đổi biến số để tính toán.
– Công thức tích phân từng phần như sau:
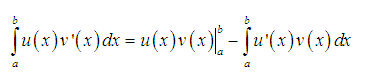
– Xét ví dụ:
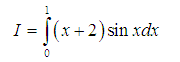
Tính tích phân sau:
Lời giải: Ta dùng cách đặt u(x) theo thứ tự ưu tiên sau:
“Nhất lô – nhì đa – tam lượng – tứ mũ”
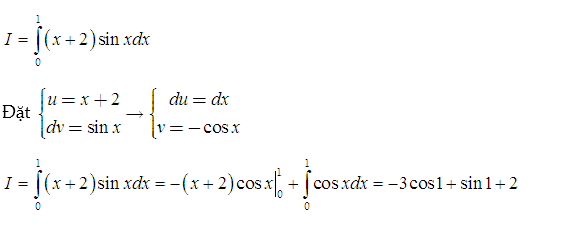
Một số sai lầm khi tính tích phân thường mắc phải
Các bài tập tính toán liên quan nội dung tích phân có thể khá dài dòng, chỉ cần một số thiếu sót rất nhỏ cũng sẽ làm bài toán cho ra kết quả sai. Vậy những sai lầm cần tránh khi tính tích phân là gì?
1/ Đổi biến nhưng không đổi cận
2/ Đổi biến nhưng không tính vi phân
3/ Tính sai nguyên hàm và hiểu sai bản chất công thức
Trên đây là tổng hợp những nội dung quan trọng liên quan đến chủ đề: Tích phân là gì – Phương pháp tính tích phân. Mong rằng bài viết thực sự mang lại những kiến thức giải tích bổ ích cho bạn đọc!
Xem thêm: